Originally published on 17/03/2018, and updated 09/09/2023
Us humans are governed by the relentless tick-tock of time.
And we constantly have to choose.
Some of these decisions require us to consider multiple options over time – like dating, househunting or jobseeking.
But we only have so much capacity with which to make each decision.
Each choice comes with its own emotional and cognitive price tag.
Whether it's viewing potential houses, driving round and round car parks for the ideal spot, or weathering the ups and downs of dating – every moment spent "looking" siphons our energy.
We're allocating time, energy and emotional labour – and we end up with things like decision fatigue, fear of missing out (FOMO, if you will), dread of regret and all kinds of other neuroticisms which come with the human condition.
So, how should we know when to stop looking and start leaping? Indeed, when will anyone?
The Optimal Stopping Problem
When should we stop looking and when to start leaping?
We all have to answer this question during the course of our lives, whether it be searching for a new home, hiring an employee or searching for a great car parking spot in a busy car park.
This is called the Optimal Stopping Problem.

This space'll do. Credit: Author, Midjourney
Let's stick with the theme of romantic matchmaking for a moment.
How will we know when we have met enough people to know who our best match is? It’s plainly true that gathering as much data as possible is the most helpful way to establish who our best match is.
But this doesn’t take into account the very nature of the human condition: being subject to time. By the time we’ve gathered the data, the chance to romantically whisk away our first choice has almost certainly passed.
So how do we balance this desire to be matched with the best possible person with the desire to find that person before it’s too late?
Or our desire to get the best car parking spot in a heaving car park, without driving around in loops for hours?
When should we stop?
The 37% Rule
Let’s say you’re 20 years old and want to marry when you’re 30, and that in that time it’s realistic for you to date 1 person every year.
You could date 10 people in that time.
Now, if you were to marry the first person you dated, your odds of marrying the best person would be 10% — certainly not outstanding.
To get a sense of what’s out there, you would need to date a few more people.
In fact, according to the 37% rule, you shouldn’t marry the first 3 people you date.
However, after 37% of the time has passed between your twentieth and thirtieth birthdays, you should aim to marry the next person who is as least as wonderful as the best person you dated beforehand.
Stopping optimally means selecting the next best choice after seeing and eliminating 37% of your options.
The applications for this knowledge don’t stop at finding love. We can apply optimal stopping to all kinds of situations, including buying a house, hiring, shopping (for say, a new laptop), picking a film to watch and much more.
A useful nuance of the optimal stopping rule is that you can choose whether to apply it based on the number of attempts (interview 100 people, “leap” after 37) or based on the time taken (interview for 100 days, “leap” after 37). Your success rate will remain the same.
The Best Possible Outcome?
Optimal stopping doesn't guarantee the best possible outcome.
It just optimises your chances of getting the best possible outcome, 37% of the time.
If you’ve decided you’re only going to interview 2 people before “leaping”, this doesn’t sound very impressive. But what if you were willing to interview 15? 37% would be strong odds indeed!

What if you could — hypothetically — interview a million people? As bizarre and counterintuitive as this may seem, your odds are still 37%. And that’s surely incredible.
No matter how many options you consider or how long you look for, your chances of selecting the best possible outcome will always be 37%.
How Maths Makes the Magic Happen
The 37% rule comes from probability theory in maths – specifically, it's derived from the Secretary Problem.
It uses a special number called Euler's number or e – an irrational number with a value of approximately 2.718 – which is a number that shows up a lot in disciplines like probability and finance (a little like how Pi is special when we talk about circles). In the 37% rule, we divide 1 by e. We get about 0.368, or 36.8% – approximated to 37%.
In the graph below, the x-axis represents the sequence of our choices.
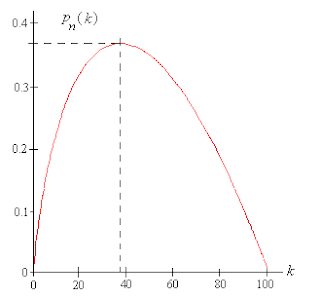
The high point, marked by a vertical line, is 37% of the way through those choices. It's your optimal stopping point.
To the left of the line is where you're looking.
To the right of the line is where you switch to leaping.
This high point is determined by 1/e, that special number in probabilities.
So, the next choice that is better than any in the looking phase is likely your best bet.
Earlier, I explained that no matter how many options you consider or how long you look for, your chances of selecting the best possible outcome will always be 37%.
This remarkable property of the 37% rule arises from its alignment with the "law of large numbers".
Roughly, this principle says that the more data we gather, the closer we get to a reliable or "true" outcome. In the context of the 37% rule, however, the surprising thing is that its effectiveness remains consistent as we scale. That's remarkable in itself.
Wrapping Up
Whilst optimal stopping isn’t foolproof, next time you’re searching for something, you will know how to get maths on your side to optimise your chances of getting the very best partner, house, new job or parking space!
I first discovered optimal stopping in Brian Christian and Tom Griffiths’ excellent book Algorithms To Live By, which I could not recommend more highly.
You might enjoy Professor Michael Trick’s entertaining blog post on his experience of Finding Love Optimally!



